9 famosi paradossi che vi manderanno in tilt il cervello

Il paradosso è uno dei meccanismi logici più sconvolgenti. Quante volte siamo rimasti sbigottiti di fronte alla celebre frase di Socrate "So di non sapere"? Ebbene, questo articolo si propone di spiegare alcuni famosi paradossi logici che hanno fatto arrovellare le menti più brillanti.
Come al solito, le soluzioni saranno elencate in ordine alla fine dell'articolo, in modo da permettere a voi lettori di concentrarvi sulla complessità dei singoli paradossi e di lasciarvi stupire dalla loro apparente insolubilità.
1. Paradosso del barbiere

Clker-Free-Vector-Images/ Pixabay
In un villaggio in cui ci sia un unico barbiere, sempre ben sbarbato e curato, il quale si prenda l'incarico di rasare tutti e solo gli uomini che non si radono da soli, chi si occupa della rasatura del barbiere?
2. Paradosso della Tromba di Torricelli

La Tromba di Torricelli è un solido creato da una funzione matematica che dà luogo ad uno strano paradosso. Esso risulta avere infatti un volume finito ed una superficie infinita, due parametri inconciliabili a livello logico.
3. Paradosso della nave di Teseo

La nave sulla quale Teseo e i suoi ritornarono da Creta aveva trenta remi e venne conservata dagli Ateniesi. L'opera di conservazione prevedeva una continua sostituzione dei remi e delle tavole di legno consumate con altre nuove e resistenti. Mentre molti consideravano la nave un oggetto storico, altri la rifiutavano dicendo che non era più la stessa nave, bensì un'altra completamente diversa fatta di materiale differente e appartenente agli Ateniesi, non più a Teseo.
4. Paradosso del Comma 22

Formulato dallo scrittore americano Joseph Heller, il paradosso del Comma 22 analizza una contraddizione dei regolamenti per i piloti. La norma in questione dice: "Chi è pazzo può chiedere di essere esentato dalle missioni di volo, ma chi chiede di essere esentato dalle missioni di volo non è pazzo". In effetti, chi fa richiesta di esenzione non può essere pazzo, poiché risulta perfettamente consapevole dei propri stati interni.
5. Paradosso di Achille e la tartaruga

Zenone costruì nel V secolo a.C. questo famoso paradosso: un corpo in veloce movimento, Achille, non può raggiungerne uno più lento, la tartaruga; per raggiungerla, Achille deve prima arrivare ad un punto intermedio in cui lei si trovava, ma mentre ci arriva lei si è spostata, seppur di poco. Procedendo così all'infinito, ne consegue che Achille, a livello logico-matematico, non raggiungerà mai la tartaruga.
6. Paradosso della freccia
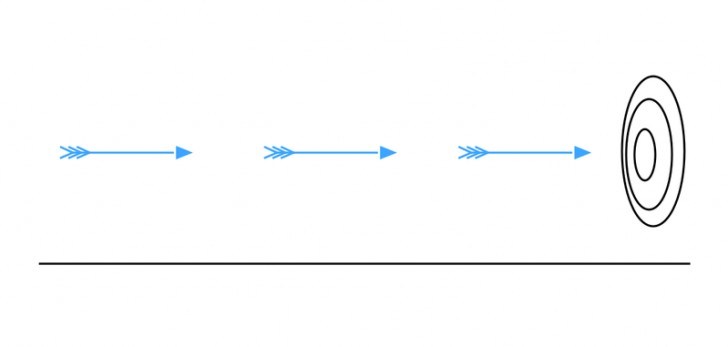
Secondo Zenone, una freccia scagliata contro un bersaglio risulterebbe immobile se osservata all'interno di ognuno degli istanti che compongono il suo spostamento - si pensi ad una serie di fotogrammi della stessa scena accostati l'uno all'altro. Dunque, conclude Zenone, il movimento della freccia è apparente, poiché essa è ferma nei singoli istanti ed appare in moto solo a causa dell'accostamento (statico) di questi ultimi.
7. Paradosso del nonno

Si tratta di un famoso paradosso che riguarda i viaggi nel tempo. Un uomo riesce a mettere a punto una macchina del tempo e torna indietro di alcuni decenni, uccidendo suo nonno. La situazione è quindi: ho viaggiato indietro nel tempo; ho ucciso mio nonno; se ho ucciso mio nonno, non esiste mio padre, e quindi non esisto io; ma se io non esisto, come ho potuto uccidere mio nonno?
8. Paradosso dei numeri interessanti

Il paradosso parte dal presupposto che ci sia qualcosa di "interessante" in ogni numero: 1 è il primo numero naturale diverso da zero; 2 è il numero primo più piccolo; 3 è il primo numero dispari; 4 è il numero composito più piccolo, e così via. Una volta approdati ad un numero privo di interesse, questo diverrebbe interessante in quanto 'primo numero privo di interesse'. Una situazione a dir poco paradossale!
9. Paradosso dei compleanni

Rinchiudendo ventitré persone all'interno di una stanza, c'è una buona possibilità che almeno due di loro festeggino il compleanno lo stesso giorno. Perché?
Ecco le soluzioni:
1. In ogni caso si cade in una contraddizione: se il barbiere si radesse da solo, non sarebbe vero il presupposto secondo cui lui rade solo gli uomini che non si radono da soli; se lo radesse qualcun altro, dovrebbe essere rasato dal barbiere, che è lui stesso.
2. Il solido può essere immaginato come la riduzione di un solido tridimensionale ad una linea bidimensionale. La linea, essendo un oggetto geometrico privo di volume, estenderebbe la superficie della Tromba senza ampliarne il volume.
3. Il paradosso nasce dalla contrapposizione tra sostanza e forma: la nave ha lo stesso aspetto, ma le molecole e gli atomi che la compongono sono diversi. È lo stesso oggetto oppure no?
4. Il paradosso non fa parte realmente del codice di aviazione, ma viene soltanto ipotizzato in un libro. La sua insolvibilità logica, però, rimane evidente.
5. Il paradosso appare irrisolvibile se si parte dal presupposto che lo spazio che separa Achille e la tartaruga possa essere frazionato all'infinito. La meccanica quantistica spiega invece che c'è una scala minima della materia, quella delle particelle fondamentali, le quali non possono ulteriormente essere divise.
6. Per risolvere tale paradosso, basterebbe smettere di pensare al tempo come ad una serie di istanti immobili.
7. Il paradosso dimostra l'impossibilità di viaggiare nel tempo nel passato, a meno che non si presupponga (come molti hanno obiettato) che ad ogni viaggio si generi un universo parallelo.
8. Il paradosso nasce da una definizione labile del termine "interessante". Nel 2009 la ricercatrice Nathaniel Johnson ha definito numeri interessanti tutti quelli presenti nella On-Line Encyclopedia of Integer Sequences, che raccoglie decine di migliaia di sequenza matematiche (Fibonacci, Pitagora, ecc.); ha così trovato il primo numero non interessante, ovvero 11.630; a causa della continua creazione di nuove sequenze, nel 2013 tale numero è stato aggiornato con 14.228.
9. Dipende tutto dalla statistica. Secondo i calcoli, raggiunte le ventitré persone la possibilità che tutte e ventitré abbiano compleanni diversi scende a meno del 50%!