I ricercatori hanno finalmente scoperto perché la musica di Bach suona così bene

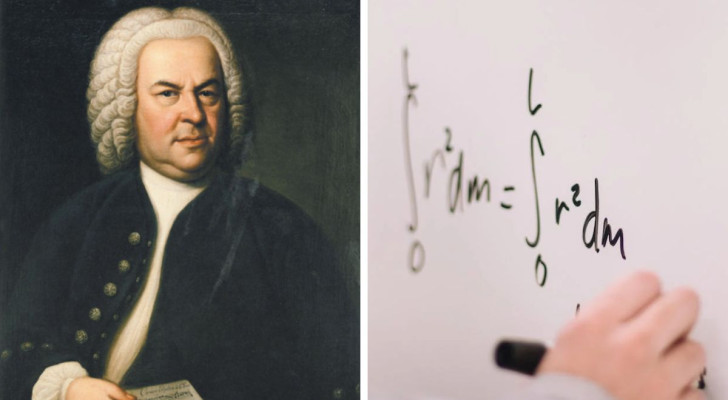
La musica è considerata da molti un linguaggio universale, in senso metaforico o meno, e lo stesso può dirsi della matematica. I collegamenti fra le due discipline non sono qualcosa di nuovo, ma un fisico ha deciso di indagare il rapporto fra musica e matematica dal punto di vista nuovo della teoria delle reti e dell'entropia. Partendo dalle composizioni di Johann Sebastian Bach, ma con implicazioni nel futuro della musica e non solo.
La teoria delle reti e la musica

Pexels
Quando si parla della musica come linguaggio universale ci si riferisce al suo portato emotivo. La musica non è soltanto emozione, ma anche informazione. Da questa semplice affermazione, alcuni studiosi dell’Università della Pennsylvania hanno cercato di misurare la quantità di informazione presente nei brani musicali. Più in particolare, hanno sviluppato uno strumento basato sulla teoria delle reti per analizzare il repertorio del compositore barocco Johann Sebastian Bach, con risultati inaspettati.
Infatti, questo approccio ha permesso ai ricercatori di studiare il contenuto di informazione dei brani di Bach. L’obiettivo è scoprire quali siano le caratteristiche che permettono la trasmissione delle informazioni a chi quei brani li ascolta. Ed è proprio per affrontare la complessità delle composizioni musicali che ci si è rivolti alla teoria delle reti, utile a comprendere i sistemi interconnessi.
Qual è l’informazione dei brani composti da Bach?
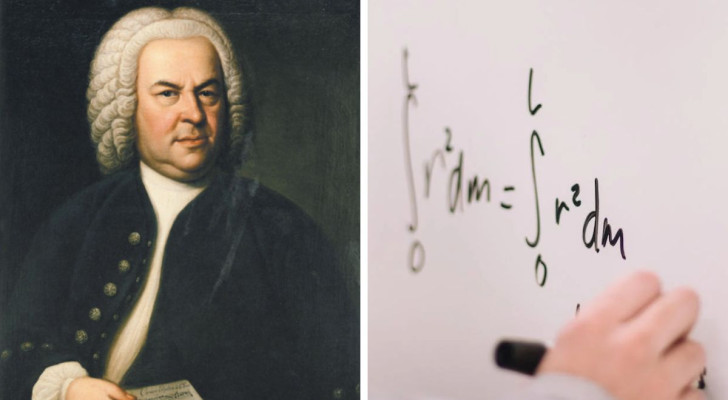
Wikimedia Commons - Public Domain / Pexels
Ma di cosa parliamo quando parliamo di teoria delle reti applicata alla musica? Nel loro studio su Bach, i ricercatori hanno creato delle rappresentazioni dei brani in cui ogni nota è rappresentata da un nodo collegato ad altri nodi, ossia altre note. In particolar modo, ci si è concentrati sulle transizioni da una nota all’altra, cercando di ricavare il contenuto di informazione dei brani composti da Bach. Attribuendo pesi e spessori diversi ai nodi, è stato possibile rendere conto della frequenza con cui queste transizioni si verificano.
I risultati sono stati senza dubbio inaspettati, ma anche decisamente interessanti. Per esempio, i corali sono brani semplici e prevedibili realizzati per il canto in chiesa, e pertanto hanno un basso contenuto informativo. In gergo, secondo le analisi dei ricercatori, possiamo dire che hanno una bassa entropia. Toccate e preludi invece sono brani più complessi e sorprendenti, pertanto comunicano una maggiore ricchezza di informazione.
Dalla descrizione dei brani alla predizione: la teoria delle reti al servizio della musica

Pexels
Come si può vedere dal testo, i risultati del team di ricercatori sono stati prettamente descrittivi. Hanno cioè analizzato alcuni brani di Bach andando a trovare corrispondenze fra l’uso della teoria delle reti, l’entropia, il contenuto di informazione e l’effetto sull’ascoltatore. Il lavoro potrebbe tuttavia essere ampliato per includere anche altri aspetti della musica, come il ritmo e il timbro, usando reti multistrato. Da qui, potrebbe essere possibile confrontare composizioni diverse e forme d’arte diverse. Ma a cosa serve?
L’idea è quella di passare dall’approccio descrittivo a quello predittivo: utilizzare la teoria delle reti, in pratica, per aiutare i compositori durante il processo creativo. Un software di nuova generazione, per esempio, potrebbe valutare diversi gradi di entropia e indirizzare il compositore verso modifiche mirate per ottenere l’effetto desiderato. D’altronde, si sa, alla base della musica c’è la sottile dinamica fra aspettativa e sorpresa. E quello sì che è un linguaggio universale.